Optique des LASER et faisceaux gaussiens
II. Stabilité des cavités Lasers
4. Stabilité d'une cavité
Étude générale
Considérons une cavité représentée par une structure périodique d'éléments optiques. La matrice de transfert de l'ensemble est \( T = \begin{pmatrix} A & B \\ C & D \\ \end{pmatrix}\).
Pour \(n\) périodes, soit \(n\) aller-retours dans le cas d'une cavité linéaire, la matrice de transfert est \(T^n\). Si on note \(p_0 = \begin{pmatrix}h_0 \\ \theta_0 \end{pmatrix}\) le vecteur représentant un rayon à l'entrée de la séquence, et \(p_n = \begin{pmatrix}h_n \\ \theta_n \end{pmatrix}\) le vecteur à la sortie, on a \(p_n = T^n p_0\).
La matrice \(T\) est diagonalisable, et si on note \(P\) la matrice de passage unitaire et \(x_{1,2 }\) les deux valeurs propres de \(T\), on a \(T=P \begin{pmatrix} x_1 & 0 \\ 0 & x_2 \end{pmatrix} P^{-1}\).
On en déduit donc que \[p_n=P \begin{pmatrix} x_1^n & 0 \\ 0 & x_2^n \end{pmatrix} P^{-1}p_0\]
Pour que la cavité soit stable, il faut que les rayons restent au voisinage de l'axe optique au cours de la propagation à travers les n éléments quand n tend vers l'infini. Autrement dit, il faut que \(p_n\) soit borné supérieurement, ou encore que \(\lvert {x_1} \rvert \leq 1\) et \(\lvert{x_2}\rvert \leq 1\)
Par ailleurs, les valeurs propres \(x_1\) et \(x_2\) de \(T\) obéissent aux relations suivantes (voir cours d'algèbre linéaire): \[x_1x_2 = \lvert T \rvert = 1\ (T\ est\ unitaire)\] \[x_1+x_2=Trace(T)=A+D\]
Comme \(x_1\) est à priori un complexe, on pose \(x_1 = \lvert x_1 \rvert e^{i\phi}\) et par suite \(x_2 = \lvert x_1 \rvert ^1 e^{i\phi}\)
Donc comme \(\lvert {x_1} \rvert \leq 1\) et \(\lvert{x_2}\rvert \leq 1\), on a forcément \(\lvert {x_1} \rvert = \lvert{x_2}\rvert = 1\). Ensuite, la relation faisant intervenir la trace de \(T\) conduit à \(2 cos(\phi)=A+D\).
On en déduit la condition de stabilité applicable à toute cavité :, \[-1\leq \frac{A+D} 2 \leq 1\] ou encore \[0 \leq \frac {A+D+2} 4 \leq 1\]
Définition:
Une cavité est stable quand les coefficients de sa matrice vérifient la condition de stabilité énoncée ci-dessus.
Exemple d'application
Prenons une cavité linéaire simple de longueur \(d\) à deux miroirs de rayons de courbures \(R_1\) et \(R_2\), équivalente à une séquence périodique de deux lentilles minces de focales \(f_1 = \frac {R_1} 2 \) et \(f_2 = \frac {R_2} 2\), séparées d'une distance \(d\).
La matrice T vaut (voir figure 4): \[ T = \begin{pmatrix} 1 & 0 \\ \frac {-1}{f_1} & 1 \end{pmatrix} \begin{pmatrix} 1 & d \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ \frac {-1}{f_2} & 1 \end{pmatrix} \begin{pmatrix} 1 & d \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1-\frac d {f_2} & d\left(2-\frac d {f_2}\right) \\ \frac {-1}{f_1}-\frac {1}{f_2}+\frac {d}{f_1f_2} & \left(1-\frac d {f_1}\right)\left(1-\frac d {f_2}\right) - \frac d {f_1} \end{pmatrix}\]
On montre alors facilement que\[\frac{A+D+2}4=\left(1-\frac d{R_1}\right)\left(1-\frac d{R_2}\right)\]
On a l'habitude de poser \(g_i=1-\frac d {R_i}\) et on obtient la condition de stabilité de la cavité pour une cavité linéaire à deux miroirs : \[0\leq g_1g_2 \leq 1\]
On visualise classiquement cette condition de stabilité sur un diagramme représentant l'espace \(g_2(g_1)\), c'est à dire en prenant \(g_2\) comme axe des ordonnées et \(g_1\) comme axe des abscisses (figure 7).
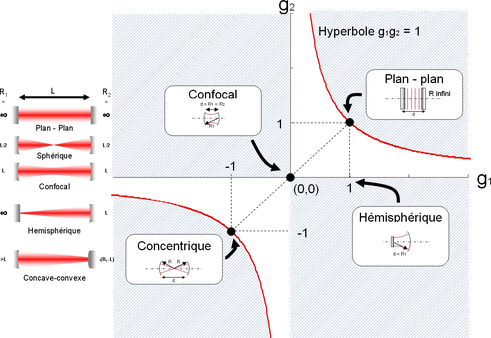
Figure 7 : Conditions de stabilité pour une cavité linéaire à deux miroirs et exemple de cavités classiques.
La condition de stabilité est alors représentée par deux hyperboles, et les zones d'instabilité sont hachurées sur la figure.
Quelques cas particuliers sont remarquables :
- Sur l'hyperbole \(g_1g_2=1\): on a alors \(d=R_1+R_2\), ce sont les cavités dites concentriques.
- Les droites \(g_1=1\) et \(g_2=1\) correspondent à des cavités où l'un des miroirs est plan (rayon de courbure infini). La cavité Fabry-Pérot (2 miroirs plans) est obtenue pour \(g_1=g_2=1\).
- Pour \(R_1 = R_2 = d\ (g_1 = g_2 = 0)\), on a une cavité dite « confocale ».
Remarque:
Il existe une méthode graphique, dite « méthode des cercles de Deschamps », qui permet de savoir si une cavité à deux miroirs sphériques est stable : il suffit de vérifier que les deux cercles de diamètres \(R_1\) et \(R_2\) centrés sur les points focaux \(F_1\) et \(F_2\) se coupent (voir figure 8). Si c'est le cas, la cavité est stable (on peut vérifier que cela est une conséquence directe de la formule établie plus haut).
Les cercles de Deschamps permettent également d'avoir accès (voir figure 8) à la position du « waist » (intersection des cercles) et à la « longueur de Rayleigh » \(Z_R\) , deux paramètres qui seront définis dans la suite de ce cours.
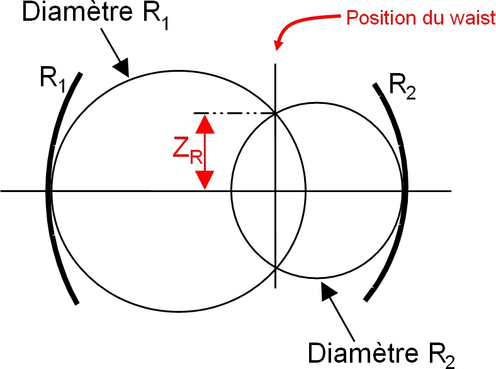
Figure 8 : Cercles de Deschamps
Il n'est pas obligatoire de disposer d'une cavité stable pour obtenir un effet laser. Dans certains cas, lorsque le gain du milieu laser est suffisant pour permettre des pertes très élevées, les résonateurs instables présentent des avantages importants. C'est en particulier le cas des lasers de très haute puissance.
Cavités instables
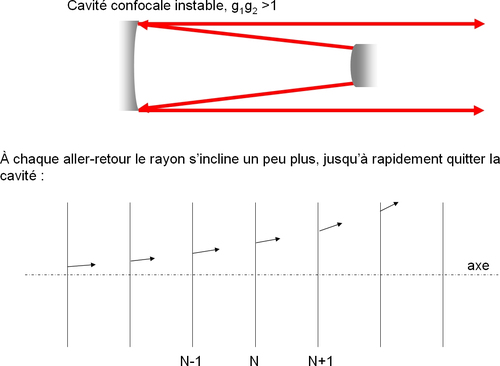
Figure 9 : Exemple de cavité instable hémisphérique
L'avantage principal de ces cavités est que le volume du mode dans la cavité peut être important, ce qui diminue la densité de puissance sur les miroirs (important pour les lasers de fortes puissances, où les seuils de dommage sont rapidement atteints). De plus, les modes transverses subissent de très fortes pertes, et ces cavités oscillent donc naturellement sur leur mode fondamental en général.
Ces cavités ne sont possibles qu'avec des milieux à très fort gain puisqu'un rayon donné ne fait que quelques passages dans le milieu amplificateur avant de s'échapper de la cavité.