Optique des LASER et faisceaux gaussiens
I. Les résonateurs ouverts
3. Modes spectraux et modes longitudinaux
On peut définir les modes d'un résonateur ouvert en utilisant les expressions bien connues pour les résonateurs fermés : dans le cas du parallélépipède défini par les longueurs de ses trois côtés \(a, b, d\), les fréquences \(\nu_{mnq}\) sont données par \[\nu_{mnq} = \frac c 2 \sqrt{\left( \frac m a \right) ^2 + \left( \frac n b \right) ^2 + \left( \frac q d \right) ^2}\] où \(c\) est la vitesse de la lumière dans le vide.
Dans le cas d'un résonateur ouvert, \(d\gg (a,b)\) et en prenant \(a=b\) pour simplifier l'expression , on obtient \[\nu_{mnq} = \frac {qc}{2d} \sqrt{1+\frac {n^2 + m^2}{a^2} \frac{d^2}{q^2} }\] ou encore après développement limité \[\nu_{mnq} \approx q \frac {c}{2d} + (m^2 + n^2) \frac{cd}{4qa^2}\]
On a ainsi une expression des fréquences des modes \(TEM_{mnq}\).
Les modes longitudinaux sont les modes \(TEM_{00q}\). Leur fréquences valent \(\nu_q = q \frac c {2d}\) et on les appellent aussi parfois « modes spectraux » (voir figure 2).
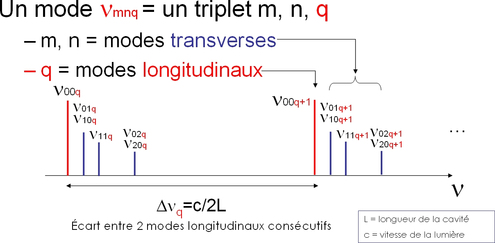
Figure 2 : Modes longitudinaux et transverses dans une cavité résonante.
Deux modes longitudinaux sont donc séparés de \(\Delta \nu_q = \frac c {2d}\) soit pour \(d\)=10 cm un écart fréquentiel de 1,5 Ghz.
Définition:
Lorsqu'on parlera d'un laser « monomode longitudinal », on fera référence à un laser ayant une fréquence bien définie (\(q\) fixé). Un seul mode longitudinal sera autorisé à osciller, ce qui conférera au susnommé laser une grande pureté spectrale ainsi qu'une longueur de cohérence importante
Les modes transverses sont les modes \(TEM_{mnq}\) avec \(m\) et/ou \(n\) différents de zéro (et presque toujours inférieurs à 10, rappelons que c'est le but du résonateur ouvert d'avoir un nombre de mode réduit).
Définition:
Un laser est dit « monomode transverse » lorsque seuls les modes \(TEM_{00q}\) lasent.
L'intervalle spectral entre deux modes transverses de n et q fixés vaut \[\delta\nu_m = (2m+1)\frac{cd}{4qa^2}\]
La répartition spectrale des modes longitudinaux et des premiers modes transverses est donnée sur la figure 2. On note que les modes \(m^2+n^2=constante\) sont dégénérés.
Remarque:
Cette analyse est valable dans le cadre d'une approche «ondes planes». On verra par la suite que les expressions sont différentes pour des faisceaux gaussiens.
Exemple:
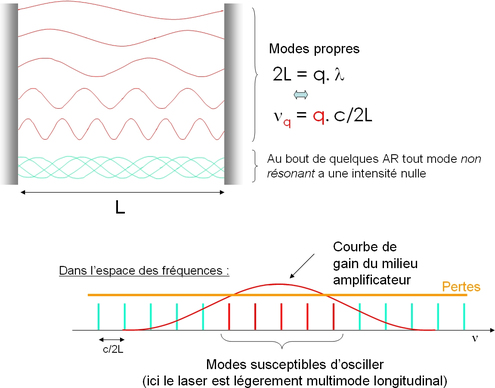
Figure 3 : Répartition spectrale des modes longitudinaux d'un laser
Quelle est la largeur spectrale d'un laser faiblement multimode ? Et d'un laser monomode ?
Considérons une cavité de 15 cm de longueur optique. L'écart entre deux modes consécutifs est \(\frac c {2L}\), soit ici 1 GHz. Si on considère que 5 modes sont susceptibles d'osciller (cas de la figure 3) on obtient une largeur spectrale en fréquence de 5 GHz, ou encore en passant en longueur d'onde de 17 pm. C'est bien inférieur à la résolution de la plupart des spectromètres : le laser apparaît monochromatique (même si en toute rigueur il n'est pas monomode).
Pour certaines applications (métrologie...) on a besoin de lasers plus fins spectralement : on peut alors forcer le comportement monomode (par exemple en diminuant les pertes pour un seul des modes susceptibles d'osciller). La largeur spectrale obtenue est alors la largeur naturelle d'une seule raie laser, qui dépend beaucoup du type de milieu laser employé (gaz, solide...), et dont l'ordre de grandeur peut varier de quelques Hz au MHz et plus.