Optique des LASER et faisceaux gaussiens
V. Les modes d'ordre superieur
2. Modes Hermite-Gaussien
Structure du champ électromagnétique
Commençons par nous limiter aux modes relatifs à des coordonnées cartésiennes, liés à une géométrie rectangulaire.
On peut alors écrire une solution de l'équation d'onde sous la forme : \[\psi(x, y, z) = g\left(\frac xw\right) h\left(\frac yw\right)e^{-i\left(\Delta\phi(z)+\frac k{2q(z)}(x^2+y^2\right)}\] où \(g\) (resp. \(h\)) est une fonction de \(z\) et de \(x\) (resp. de \(z\) et de \(y\)).
En intégrant cette solution dans l'équation d'onde paraxiale, on obtient une équation différentielle pour \(g\) et \(h\) qui admet pour solution des polynômes d'Hermite.
On peut montrer (mais on ne le fera pas ici) que l'on obtient un ensemble complet de solutions sous la forme : \[E_{mn}(x, y, z)=\sqrt{\frac 2\pi \frac 1{2^{m+n}}\frac 1{m!n!}}\frac 1w(z)H_m\left(\frac{\sqrt 2 x}{w(z)}\right)H_n\left(\frac{\sqrt 2 y}{w(z)}\right)e^{-i(kz-\phi(z))}e^{-i\left(\frac k{2q}(x^2+y^2)\right)}\] où :
- \(m, n\) sont des entiers
- \(q, R, w\) sont les mêmes que ceux définis pour le mode fondamental gaussien
- \(\phi(z)=(m+n+1)arctan\left(\frac {\lambda z}{\pi w_0^2}\right)\)
- \(H_m(X)=(-1)^me^{X^2}\frac {\partial ^m}{\partial X^m}e^{X^2}=m!\sum_{p=0}^{\frac m2}\left((-1)^p\frac{(2X)^{m-2p}}{p!(m-2p)!}\right)\) le polynôme d'Hermite d'ordre \(m\)
- On a par exemple \(H_0(X) = 1, H_1(X) = 2X, H_2(X) = 4X^2-2\), ...
- Pour \(m = n = 0\), on retrouve le mode fondamental gaussien.
- Pour \(m\) et \(n\) quelconques, la loi de propagation pour \(R\), \(q\) et \(w\) est inchangée. Seuls le déphasage et la structure transverse du faisceau sont différents.
On peut observer sur les figures 19 et 20 la répartition d'intensité pour ces modes. On note la présence de « zéros », sous forme de lignes sombres, dont le nombre correspond à l'ordre considéré.

Figure 19 : Répartition spatiale de l'énergie dans les modes d'ordre supérieur à symétrie rectangulaire (1)
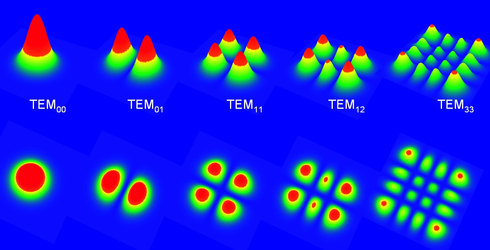
Figures 20 : Répartition spatiale de l'énergie dans les modes d'ordre supérieur à symétrie rectangulaire (2)
Spectre de fréquence pour une cavité classique à deux miroirs
Le déphasage au bout d'un aller-retour dans une cavité à deux miroirs doit être un multiple de \(2\pi\). En partant du terme de phase et en procédant comme au paragraphe intitulé "Fréquence des modes \(TEM_{00}\) dans le cavité" on obtient l'expression de la fréquence d'un mode \(TEM_{mnq}\). \[\nu_{mnq}=\frac 2{2d}\left(q+\frac 1\pi (m+n+1) arccos(\pm\sqrt{g_1g_2})\right)\] \(g_i\) est le paramètre \(1-\frac d R_i\) défini pour une cavité de longueur \(d\) et les rayons de courbure des miroirs \(R_i\). Pour \(m=n=0\) on retrouve évidemment l'expression du paragraphe "Fréquence des modes \(TEM_{00}\) dans le cavité" pour le mode fondamental.
Le spectre des fréquences dépend des valeurs des rayons de courbure :
- Regardons ce qui se passe pour un résonateur quasi-plan (\(R_1\) et \(R_2\) égaux et très grands devant \(d\)):
Le terme en \(arccos\) de l'expression ci-dessus devient \(arccos(g)\) et \(g\) est proche de 1 donc on peut écrire: \(arccos(g)\approx\sqrt\frac {2d}R \ll 1\). Les fréquences \(\nu_{mnq}\) sont très proches des fréquences \(\nu_{00q}\). L'intervalle spectral \(\delta\nu\) pour \(\Delta m =1\) ou \(\Delta n =1\) vaut \(\frac 1 \pi \sqrt \frac{2d}R\frac c{2d}\) soit quelques dizaines de MHz environ.
- Pour une cavité symétrique quasi-confocale (\(R_1 = R_2 = d\)) on trouve un écart entre les modes de \(\frac c{4d}\) et une dégénérescence des fréquences (les modes longitudinaux et certains modes transverses ont la même fréquence).