Optique des LASER et faisceaux gaussiens
IV. Mode fondamental Gaussien et cavité laser
2. Cavité à deux miroirs
Introduction
Nous allons étudier plus en détail la cavité classique à deux miroirs sphériques de rayons de courbure \(R_1\) et \(R_2\) distants de \(d\).
Géométrie de la cavité
Si un faisceau gaussien est un mode d'un tel résonateur, alors nécessairement son rayon de courbure est égal (en valeur absolue) au rayon de courbure des miroirs au niveau de ces derniers. C'est une condition indispensable pour assurer le retour sur lui-même du faisceau.
Si on appelle \(z_1\) et \(z_2\) les positions des miroirs \(M_1\) et \(M_2\) respectivement, on a donc \(R(z_1) = -R_1\) et \(R(z_2) = R_2\).
Remarque :
Attention aux conventions de signe: ici on prend \(R>0\) pour une onde divergente et \(R<0\) pour une onde convergente
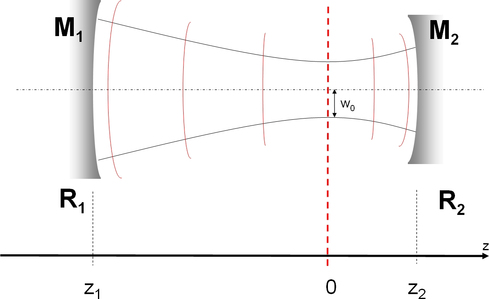
Figure 16 : Géométrie de la cavité utilisée pour la démonstration
Grâce à cette propriété, on peut déterminer la géométrie du mode dans la cavité sans passer par la loi ABCD générale : il suffit d'appliquer les relations démontrées pour l'onde sphérique gaussienne (fin du paragraphe sur l'"Onde Sphérique Gaussienne") en choisissant comme origine le waist du faisceau (qu'on cherche à déterminer).
On écrit alors \[-R_1=R(z_1)=z_1\left(1+\left(\frac{\pi w_0^2}{\lambda z_1}\right)^2\right)=z_1+\frac{Z_R^2}{z_1}\] et \[R_2 = R(z_2) = z_2+\frac{Z_R^2}{z_2}\] qui sont les conditions aux limites sur les miroirs. On a également \(z_2-z_1=d\). Il suffit de résoudre ce système de trois équations à trois inconnues \(z_1\), \(z_2\) et \(Z_R\) afin d'obtenir leurs valeurs en fonction des rayons de courbure des deux miroirs et de la distance \(d\).
En faisant (c'est un bon exercice) le calcul in extenso, et en notant à nouveau \(g_i=1-\frac d{R_i}\) avec \(i=1, 2\), on obtient l'ensemble des relations suivantes : \[z_1 = \frac{d(d-R_2)}{R_1+R_2-2d} = \frac{-dg_2(1-g_1)}{g_1+g_2-2g_1g_2}\] \[z_2 = \frac{d(R_1-d)}{R_1+R_2-2d} = \frac{-dg_1(1-g_2)}{g_1+g_2-2g_1g_2}=z_1+d\] \[Z_R^2 = \frac {d(R_1+R_2-d)(R_1-d)(R_2-d)}{(R_1+R_2-2d)^2}=\frac {d^2g_1g_2(1-g_1g_2)}{(g_1+g_2-2g_1g_2)^2}\] \[w_0 = \sqrt \frac \lambda \pi \sqrt[4]{\frac {d(R_1+R_2-d)(R_1-d)(R_2-d)}{(R_1+R_2-2d)^2}}=\sqrt \frac{\lambda d}\pi \sqrt[4]{\frac {g_1g_2(1-g_1g_2)}{(g_1+g_2-2g_1g_2)^2}}\]
On peut retrouver ici la condition de stabilité pour une cavité à deux miroirs déjà démontrée précédemment, à savoir \(0\lt g_1g_2\lt 1\) avec cette fois-ci des inégalités strictes.
Pour généraliser le diagramme de stabilité de la figure 7 aux faisceaux gaussiens, il faut donc exclure l'hyperbole elle-même et les axes \(g_i = 0\).
L'exemple le plus simple est la cavité Fabry-Pérot à deux miroirs plans dont les éléments de matrice \(A\) et \(D\) valent 1 (ou encore \(g_1 = g_2 = 1\)): la condition de stabilité est vérifiée dans ce cas si on utilise l'expression de l'optique géométrique, mais ne l'est pas pour des faisceaux gaussiens. Une telle cavité n'est pas un résonateur laser stable en tant que tel.
Il est néanmoins possible d'obtenir un laser stable avec une cavité Fabry-Pérot plan-plan, car d'autres éléments peuvent stabiliser la cavité – par exemple le milieu amplificateur lui-même peut souvent se modéliser par une lentille (d'origine thermique, due au pompage) convergente qui stabilise la cavité.
Il existe une méthode graphique pour déterminer facilement la position et la taille du waist dans une cavité à deux miroirs, basée sur les cercles de Deschamps (voir figure 8).
Fréquence des modes \(TEM_{00}\) dans la cavité
La condition de résonance d'un mode est que le champ ne change pas au bout d'un aller-retour dans la cavité. En d'autres termes, la variation de phase dans cet aller-retour doit être un multiple entier de \(2\pi\);
Le terme de phase pour une onde sphérique gaussienne vaut (voir paragraphe sur l'"Onde Sphérique Gaussienne") \(e^{ikz}e^{i\zeta (z)}\) où on rappelle que \(tan(\zeta (z)) = \frac z {Z_R}\). La première exponentielle est simplement le déphasage dû à la propagation, tandis que la deuxième est spécifique au faisceau gaussien.
Si \(\phi (z)\) est la phase en \(z\), on doit donc avoir : \[\Delta \phi = \phi (z_2) - \phi(z_1)=-k(z_2-z_1)+(\zeta(z_2)- \zeta(z_1))=-q\pi\] \(q\) est ici un nombre entier égal au nombre de demi-longueurs d'onde contenu sur la longueur \(d\) (rien à voir avec le rayon de courbure complexe !): il y a \((q-1)\) noeuds et \(q\) ventres dans la cavité (NB : les cavités de taille standard, c'est à dire macroscopique (entre le cm et le mètre), ont un \(q\) gigantesque).
Les fréquences de résonance des modes gaussiens fondamentaux \(TEM_{00q}\) dans la cavité à deux miroirs valent donc (en remplaçant \(k\) par \(\frac {2\pi \nu}c\)): \[\nu_q=\frac c{2d}\left(q+\frac 1\pi\left(arctan\left(\frac{z_2}{Z_R}\right)-arctan\left(\frac{z_1}{Z_R}\right)\right)\right)\]
Cette expression peut être reformulée en utilisant \[arctan(a)+arctan(b) = arctan\left(\frac{a+b}{1-ab}\right)\] ce qui donne après quelques calculs : \[\nu_q=\frac c{2d}\left(q+\frac 1\pi arccos(\pm\sqrt{g_1g_2})\right)\]
Remarque :
\(g_1\) et \(g_2\) sont de même signe à cause du critère de stabilité. Si ce signe commun est positif, il faut prendre le signe \(+\) dans la formule et vice versa.
On remarque que la formule obtenue ressemble à celle donnée au paragraphe "Modes spectraux et modes longitudinaux" pour une onde plane, mais possède un terme supplémentaire \(\frac c{2d}\left(\frac 1\pi arccos(\pm\sqrt{g_1g_2})\right)\). Ce terme étant ajouté à toutes les fréquences \(\nu_q\), elles sont toutes décalées de la même quantité et l'on a toujours \(\Delta \nu_q=\frac c{2d}\).
On a fait l'étude précédente dans le cas simple d'une cavité linéaire à deux miroirs. Pour des cavités plus complexes (voir figure 17 et 18) il faut calculer pour chaque faisceau gaussien se propageant librement la variation de phase sur sa longueur, et ensuite additionner les déphasages sur un aller-retour ou un tour.