Optique des LASER et faisceaux gaussiens
III. Les faisceaux gaussiens
2. Onde sphérique gaussienne
Nous allons introduire ici une généralisation des solutions mathématiques de l'équation de Helmholtz, dont nous détaillerons par la suite la signification physique.
Considérons les solutions de l'équation de Helmholtz correspondant à des faisceaux qui se propagent globalement selon \(Oz\), avec des rayons paraxiaux.
La solution s'écrit de façon générale sous la forme suivante : \[E(x, y, z) = \psi (x, y, z) e^{-ikz}\] où \(\psi (x, y, z)\) est une fonction complexe lentement variable qui représente les différences entre un faisceau laser et une onde plane homogène.
En remplaçant cette solution dans l'équation de Helmholtz et en faisant l'hypothèse que les variations de \(\psi (x, y, z)\) dans la direction \(Oz\) sont négligeables sur une distance de l'ordre de la longueur d'onde (soit \(\lambda \lvert \frac {\partial \psi}{\partial z}\rvert \ll \lvert \psi \rvert\) et \(\lambda \lvert \frac {\partial ^2 \psi}{\partial z^2}\rvert \ll \lvert \frac {\partial \psi}{\partial z}\rvert\)), on peut réécrire l'équation d'onde paraxiale sous la forme : \[\frac {\partial ^2 \psi}{\partial x^2}+\frac {\partial ^2 \psi}{\partial y^2} -2ik \frac {\partial \psi}{\partial z}=0\]
Remarque:
On retrouve ici la forme de l'équation d'onde de Schrödinger pour une particule libre dans un espace à 2D \((x,y)\) avec le temps \(t\) remplacé par \(z\).
Les solutions de l'équation d'onde paraxiale sont connues. On peut ainsi vérifier facilement qu'une fonction (il en existe d'autres) de la forme : \[\psi (x, y, z) = e^{-i\left(\Delta \phi (z) + \frac k {2q(z)}(x^2+y^2)\right)}\] est solution, avec :
- \(\Delta\phi(z)\) est un déphasage complexe (déphasage réel et changement d'amplitude avec \(z\))
- \(q(z)\) représente un rayon de courbure complexe, ou encore la variation transverse de l'amplitude et la courbure du front d'onde.
Cette solution particulière, appelée « Mode fondamental Gaussien », est la plus importante en pratique dans les résonateurs lasers. Nous allons donc la traiter en détails par la suite.
En substituant l'expression de \(\psi(x, y, z)\) dans l'équation d'onde paraxiale, on obtient que pour tout \((x,y)\) : \[\left( \frac {k^2}{q^2} (x^2+y^2) \left(\frac {dq}{dz} -1 \right) -2k \left( \frac{d\Delta\phi}{dz} + \frac i q\right)\right)\psi = 0\]
On en déduit que \(q(z)\) et \(\phi(z)\) doivent vérifier : \[\frac{dq}{dz}=1 \Rightarrow q(z)=q_0+z\ avec\ q_0=q(0)\] \[\frac{d\Delta \phi}{dz}=-\frac i q \Rightarrow \Delta\phi(z)=-i\ ln\left(\frac{q_0+z}{q_0}\right)\ si\ \Delta \phi(0)=0\]
De plus on pose \(\frac 1 {q(z)}=\frac 1 {R(z)}-i\frac {\lambda}{\pi w^2(z)}\)
On a alors \[e^{-i\Delta\phi(z)} = \frac 1 {1 + \frac z {q_0}}=\frac 1 {1+\frac z {R_0}-\frac{i\lambda z}{\pi w_0^2}}\] où les indices 0 indiquent les valeurs en \(z=0\). Si on choisit à l'origine un rayon de courbure infini (c'est à dire une surface d'onde plane), on a \(q_0=i\frac{\pi w_0^2}{\lambda}\). On peut alors facilement montrer que : \[\frac 1 {q(z)}=\frac 1 {q_0 + z} = \frac {\frac{1}{q_0}} {1+\frac z {q_0}}= \frac 1 {1+\left(\frac {\lambda z}{\pi w_0^2}\right)^2}\left(\frac 1 z \left( \frac {\lambda z}{\pi w_0^2} \right)^2-i \frac \lambda {\pi w_0^2} \right)\]
En identifiant cette dernière relation avec \(\frac 1 R -i \frac \lambda {\pi w^2(z)}\) on déduit : \[R(z)=z+\frac{Z_R^2}{z}\ avec\ Z_R=\frac {\pi w_0^2} \lambda\] \[w(z) = w_0\sqrt{1+\left(\frac z {Z_R}\right)}\]
D'autre part: \[e^{-i\Delta \phi (z)}=\frac 1 {1-\frac {iz}{Z_R}}=\frac 1 {\sqrt{1+\left( \frac z {Z_R}\right)^2}}e^{i\zeta (z)} \ ou \ tan(\zeta (z))=\frac z {Z_R}\] avec :
- \(\frac K {w(z)}\) est un facteur de normalisation
- la première exponentielle est le terme propagatif
- la seconde exponentielle est un déphasage dit « de Gouy »
- la troisième exponentielle peut être décomposée en un terme « onde sphérique » et un terme « gaussienne » en remplaçant \(q\) par son expression en fonction de \(R\) :
\[e^{-ik\frac {r^2}{2q}} = e^{-ik \frac {r^2}{2R}}e^{-\frac {r^2}{w^2}}\] où on est passé en coordonnées cylindriques (\(r^2=x^2 + y^2\))
Fondamental
Finalement, en regroupant toutes ces expressions, on obtient la relation suivante, qui est l'expression fondamentale de l'onde sphérique gaussienne : \[E(x, y, z)=K \frac 1 {w(z)} e^{-ik(z)} e^{i\zeta(z)} e^{-ik \frac {x^2+y^2}{2q} }\]
C'est là qu'apparaît le profil transverse gaussien en tout point \(z\) de l'onde considéré. Le profil d'intensité (proportionnelle au carré du champ) du faisceau gaussien sera donc (voir figure 10) : \[I(r, z) = I_0(z)e^{\frac {-2r^2}{w^2(z)}}\]
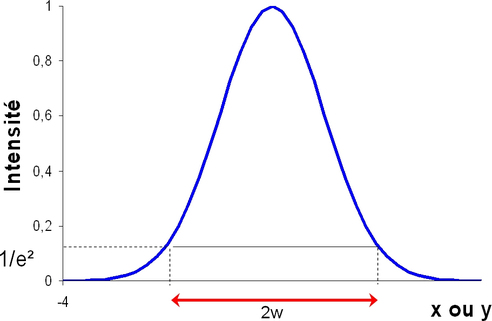
Figure 10 : Profil d'intensité gaussien.
- \(R(z) = z\left(1+\left(\frac{\pi w_0^2}{\lambda z}\right)^2\right)\) est le rayon de courbure du front d'onde qui coupe l'axe en \(z\).
- \(w(z) = w_0 \sqrt{1+\left(\frac{\lambda z}{\pi w_0^2}\right)^2}\) est une mesure de la décroissance – gaussienne - de l'amplitude du champ avec la distance à l'axe \(z\) (voir figure 10). Le paramètre \(w\) est la distance au bout de laquelle l'amplitude est égale à \( \frac 1 e\) fois sa valeur sur l'axe (\(\frac 1 {e^2}\) si on considère les intensités).
Définition :
Ce paramètre \(w\) est minimal à l'origine \(z=0\), où le rayon de courbure \(R\) est infini. Sa valeur est alors notée \(w_0\) et on parle du « waist » du faisceau (on dit parfois « col » en français)
Définition :
\(Z_R = \frac {\pi w_0^2}{\lambda}\)est appelée la longueur de Rayleigh et décrit la divergence du faisceau (voir plus loin).
On rappel aussi que :
- \(q=q_0+z\) et \(\frac 1 q = \frac 1 R -i \frac \lambda {\pi w^2}\)
- Ce déphasage signifie que l'onde gaussienne est déphasée de \(\zeta (z)\) sur l'axe \(z\) par rapport à une onde plane de même longueur d'onde « partie » depuis l'origine \(z=0\) au même instant. Ce déphasage sur l'axe spécifique à l'onde gaussienne tend vers \(\frac \pi 2\) lorsque \(z\) tend vers l'infini. Lorsque l'onde passe par \(z=0\), elle subit un déphasage global de \(\pi\).
Définition :
\(tan(\zeta)=\frac {\lambda z}{\pi w_0^2}\) et \(\zeta (z)\) est souvent appelé « déphasage de Gouy ».