Optique des LASER et faisceaux gaussiens
III. Les faisceaux gaussiens
4. Adaptation et focalisation des faisceaux gaussiens
La transformation subie par un faisceau gaussien lors de son passage dans une lentille est très souvent rencontrée expérimentalement. Lorsque l'on veut par exemple injecter un faisceau laser donné dans un autre laser pour le pomper, il importe que le faisceau soit convenablement «adapté» au résonateur du second laser.
Un faisceau gaussien est transformé en un autre faisceau gaussien par une lentille; nous allons maintenant voir comment.
En utilisant la loi ABCD (voir paragraphe sur "Les matrices de transfert et loi ABCD") appliquée à un système optique centré avec origines aux foyers, on peut trouver les relations entre les positions et les tailles d'un waist objet situé avant le système optique et celles du waist image obtenu après traversée du système.
Le « waist objet » \(w_0\) est situé sur le plan repéré par l'abscisse \(\sigma\) par rapport au foyer objet tandis que le « waist image » \(w'_0\) est repéré par l'abscisse \(\sigma '\)par rapport au foyer image (cf. figure 13).
Remarque :
Il est en toute rigueur abusif de parler de waists objet et image puisqu'au sens strict les deux waists ne sont pas conjugués l'un de l'autre. En d'autres termes, le waist du faisceau image n'est pas l'image du waist du faisceau objet. On conservera néanmoins cette terminologie dans la suite.
Le rayon de courbure complexe correspondant au waist objet est imaginaire pur et vaut: \[q_0=i\frac{\pi w_0^2}{\lambda} \]
Les éléments de la matrice de transfert du système optique valent (à vérifier à titre d'exercice) : \[A=\frac {-\sigma '}{f'};\ B=-f+\frac{\sigma \sigma '}{f'};\ C=\frac{-1}{f'};\ D=\frac \sigma {f'}\]
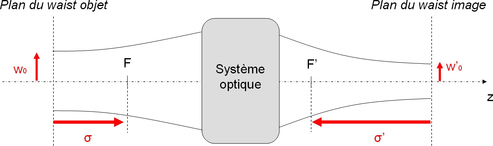
Figure 13 : Relations de conjugaison pour les faisceaux gaussiens
En appliquant la loi ABCD et sachant que \(q_0\) et \(q_0'\) sont tous les deux des imaginaires purs, on trouve les relations suivantes : \[\sigma \sigma ' = f f'-q_0q_0'\] \[-\sigma q_0' = \sigma ' q_0\] ou encore \[\sigma \sigma ' = f f'-Z_RZ_R'\] \[\frac {-\sigma}{Z_R} = \frac {\sigma '}{Z_R'}\]
Ces relations démontrent que la position du waist image dépend non seulement de la position du waist objet mais aussi de sa taille. De la même façon, la taille du waist image est fonction de la taille du waist objet et de sa position.
- Lorsque \(\sigma \gg Z_R\), l'onde au niveau du foyer objet est quasi-sphérique (celui-ci est dans le champ lointain du faisceau). L'onde vue par la lentille semble donc être émise par un point source et on obtient : \(\sigma \sigma ' = f f'\). On retrouve ici les relations conjugaison de Newton de l'optique géométrique.
- Un autre cas particulier est le cas \(\sigma = 0\), c'est à dire que le waist objet est placé au foyer de la lentille. En optique géométrique, on s'attend à avoir alors un faisceau collimaté (rayons parallèles) en sortie de la lentille. En optique gaussienne, dans ce cas, on a aussi \( \sigma ' = 0\): le waist image est situé exactement sur le foyer image.
Attention :
On voit ici que les « relations de conjugaisons » gaussiennes diffèrent sensiblement de celles de l'optique géométrique dès lors que l'on se trouve à des distances comparables à \(Z_R\) . C'est dû au fait (voir remarque précédente) que ce qu'on appelle « relation de conjugaison » ici n'en est pas une au sens de l'optique géométrique.
La relation de grandissement entre les waists est donnée dans ce cas par : \[w_0' = \frac{\lambda f}{\pi w_0}\]
C'est une relation d'une grande importance pratique car cette configuration se retrouve souvent expérimentalement. Elle permet très souvent d'obtenir un ordre de grandeur satisfaisant pour répondre à la question suivante : « quelle va être la taille du waist d'un faisceau laser après focalisation par une lentille de focale \(f\) si je connais la taille du faisceau avant la lentille ? »
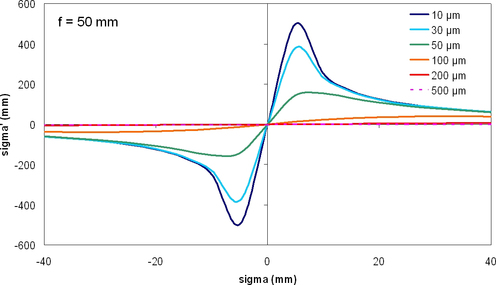
Figure 14 : Evolution de la position du waist image en fonction de la position du waist objet(pour différentes tailles du waist objet)
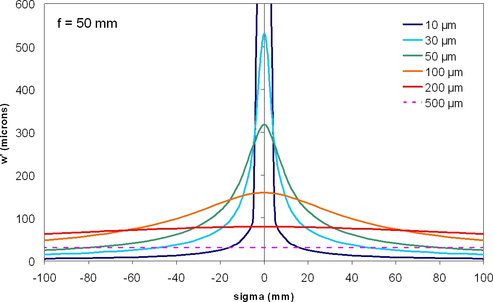
Figure 15 : Evolution de la taille du waist image en fonction de la position du waist objet (pour différentes tailles du waist objet)
En observant les figures 14 et 15 qui décrivent les équations ci-dessus, on peut faire quelques commentaires :
- Sur la figure 14, lorsque la taille du waist objet est importante, on a \(\sigma ' = 0\) quelque soit \(\sigma\): c'est le cas de l'optique géométrique où un faisceau collimaté (équivalent pour un faisceau gaussien à un faisceau de grand rayon \(w\) comme on l'a souligné plus haut) vient se focaliser dans le plan focal image de la lentille. La position du waist objet a peu de sens ici puisque la distance de Rayleigh correspondant à un grand \(w\) est très grande («collimation»).
- Lorsque la taille du waist objet est très petite (quasi ponctuelle), on se rapproche également de l'optique géométrique: on tend vers les asymptotes données par \(\sigma \sigma ' = f^2\).
- En dehors des deux cas limite précédents, le comportement s'éloigne considérablement de l'optique géométrique: ainsi pour \(w_0\) =10 µm et \(\sigma = 0\) (waist objet de petite taille au foyer objet de la lentille), on n'a pas une image à l'infini comme en optique géométrique mais une image située en \(\sigma ' = 0\), c'est à dire sur le foyer image !
- Ce « paradoxe » n'en est pas un si on regarde la figure 15 : ainsi pour \(w_0\) =10 µm et \(\sigma = 0\) (waist objet au foyer objet de la lentille), le waist image est certes sur le foyer image, mais sa taille est très importante : le faisceau est donc quasiment collimaté et on retrouve un comportement « semblable à » celui de l'optique géométrique.