Étude de cas
III. Cavité réelle
1. Optimisation de la cavité
Nous avons déterminé la géométrie du faisceau pour une longueur \(L\) fixée arbitrairement.
En pratique, cette géométrie est fixée par des conditions extérieures, notamment liées au pompage de la cavité. On a vu par exemple (voir étude de cas du grain « principes de base du laser ») que la géométrie de pompage conduisait à un rayon du faisceau de pompe fixé. Dans le cas précis décrit, le faisceau de pompe se focalise sur un ovale de dimension 20 x 100 µm en raison de l'utilisation d'une barrette de diodes laser 1 x 100 µm comme \(\Delta \nu\) pompe. Pour simplifier ici les calculs, nous supposerons que le pompage est circulaire (par exemple en utilisant une pompe fibrée), de rayon 80µm dans le cristal après passage dans les optiques de collimation/focalisation.
Il est important que le mode laser et le mode de pompe soient bien adaptés : on va donc chercher à obtenir un mode laser qui soit compatible avec la dimension du faisceau de pompe dans le cristal. Plus précisément, on va choisir de prendre un mode laser légèrement plus petit que le mode de pompe, afin d'avoir une pompe bien homogène sur toute la surface du mode de cavité.
On va donc chercher à avoir disons \(w_0\) = 60 µm.
Remarque :
On peut faire une analyse plus poussée pour déterminer quelle est la taille optimale du mode pour une géométrie de pompage donnée, mais cela est au-delà de ce cours.
Quelle est la longueur \(L\) à choisir dans ce cas, en utilisant toujours notre miroir \(R\) = 100 mm ?
Reprenons la formule \(Z_R=\sqrt{d(R-d)}=\frac{\pi w_0^2}\lambda\); on obtient un trinôme en \(d\):
\(d^2-dR+\left(\frac{\pi w_0^2}\lambda \right) ^2=0\) dont la résolution mène à deux valeurs de \(d\):
\(d_1\) = 98,85 mm et \(d_2\) = 1,14 mm.
Bien sûr seule la première conduit à une valeur ayant un sens physique (pour la seconde, \(L\) est négatif) et donne \(L\) = 93,3 mm.
On est toujours dans la zone de stabilité, mais en limite de cette dernière.
On peut tracer (figure 5) l'évolution de la taille du waist avec \(L\) pour une valeur donnée de \(R\) (ici 100 mm). Bien sûr pour \(L\gt R\) la cavité n'est plus stable et le waist n'a pas de sens.
On voit qu'il existe une zone où le waist garde une taille stable, pour \(L\) autour de \(\frac R2\) = 50 mm. On observe également qu'avec notre miroir de rayon 100 mm, il est impossible d'avoir un waist supérieur à 130 µm. Par contre on peut obtenir des waists très petits en flirtant avec la limite de stabilité.
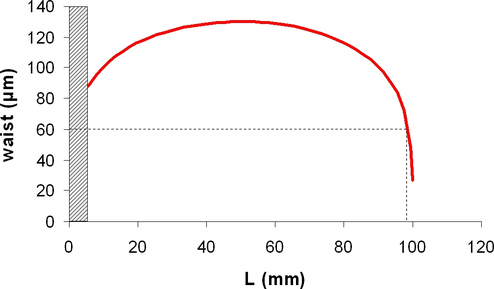
Figure 5 : Evolution du waist avec L