Optique des LASER et faisceaux gaussiens
III. Les faisceaux gaussiens
3. Propriétés des faisceaux gaussiens
La plupart des relations fondamentales liées aux faisceaux gaussiens ont été mathématiquement obtenues au paragraphe précédent. Nous allons maintenant voir leur signification physique.
Prenons comme précédemment l'origine au « waist » \(w_0\), qui correspond à l'onde plane gaussienne de rayon de courbure infini. On a défini la longueur de Rayleigh par la relation \(Z_R = \frac {\pi w_0^2}\lambda\).
On a également obtenu la loi d'évolution de \(w\) en fonction de \(z\) : \[w(z) = w_0 \sqrt{1+\left(\frac z {Z_R}\right)^2}\] \(w(z)\) est une hyperbole (on peut réécrire la relation précédente \(\frac {w^2}{w_0^2}-\frac{z^2}{Z_R^2} = 1\)).
Les principaux paramètres utiles
Rappelons les principaux paramètres utiles et leur définitions :
- \(w(z)\) est la dimension (le rayon) de la tache laser dans un plan perpendiculaire à la propagation à une distance \(z\) de l'origine. Plus précisément, c'est le rayon à \(\frac 1 e\) du profil gaussien d'amplitude transverse dans le plan d'abscisse \(z\) (à \(\frac 1 {e^2}\) si on considère le profil d'intensité : dans la formule ci-dessous, \(I=\frac {I_0}{e^2}\) pour \(r = w\)). \[I(r, z) = I_0(z)e^{\frac{-2r^2}{w^2(z)}}\]
- Le faisceau « s'étale » transversalement au cours de la propagation, tandis que son amplitude sur l'axe diminue (conservation de l'énergie). Le profil reste toujours gaussien.
- La taille du faisceau à l'origine, \(w_0\), est la taille minimale du faisceau qui diverge à partir de ce point (voir figure 11). On appelle « waist », ou encore « col » ou « taille », cette dimension minimale (NB : le waist désigne bien le rayon minimal du faisceau. Le diamètre est évidemment donné par \(2 w_0\))
- Au waist, on a vu que le front d'onde était localement plan (de rayon de courbure infini).
- La divergence du faisceau est mesurée par la limite pour \(z\) tendant vers l'infini de \(\frac w z\) : \(\lim_{z \to \infty} \frac w z = \frac {w_0}{Z_R} = \frac \lambda {\pi w_0}=tan(\theta)\) soit pour une faible divergence \(tan(\theta) = \frac \lambda {\pi w_0} \approx \theta\)
- Les propriétés « gaussiennes » du faisceau laser s'expriment essentiellement à proximité du waist. En effet, lorsque \(z\) tend vers l'infini, le rayon de courbure complexe s'identifie à \(R\) et on retrouve une onde sphérique.
- La longueur de Rayleigh est la distance (comptée en partant du waist) au bout de laquelle la taille du faisceau a augmenté d'un facteur \(\sqrt 2\) (ou encore que sa surface a doublé). C'est un paramètre important car il défini (un peu arbitrairement) la distance sur laquelle le faisceau laser garde une taille relativement constante (comprise entre \(w_0\) et \(w_0 \sqrt 2\)) - voir figure 11.
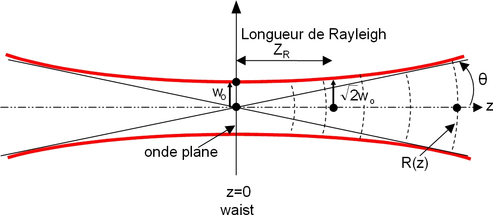
Figure 11 : Propriétés d'un faisceau gaussien
Ordre de grandeur
Remarque :
Pour un faisceau laser focalisé «assez efficacement » \(-w_0\) = 10 µm, et une longueur d'onde de 1 µm, on trouve alors \(Z_R\) = 314 µm et une divergence (demi-angle) de 1,8 degrés.
Si on prend un « gros waist » de 1 mm, on trouve alors \(Z_R\) = 3,14 m et une divergence (demi-angle) de 0,018 degrés. On a alors un faisceau que l'on qualifie généralement de « collimaté ».
Fondametal :
Plus un faisceau est gros, moins il diverge. En optique gaussienne, « collimater un faisceau » est équivalent à « obtenir un faisceau de grand waist ».
On observe l'évolution de la longueur de Rayleigh et de la divergence sur la figure 12 pour une longueur d'onde de 1 µm.
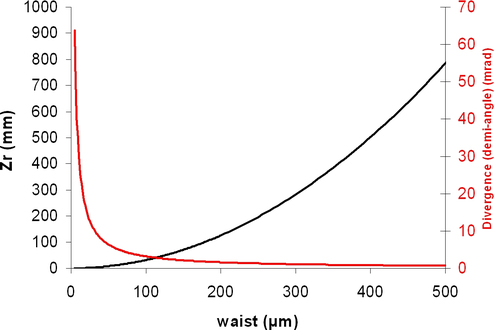
Figure 12 : Evolution de la longueur de Rayleigh et de la divergence sur la figure 12 pour une longueur d'onde de 1 µm.
Autres relations utiles
On peut déduire des relations précédentes d'autres équations utiles, comme par exemple : \[w_0^2 = \frac {w^2}{1+\left(\frac{\pi w^2}{\lambda R}\right)^2}\] et \[z = \frac {R}{1+\left(\frac{\lambda R}{\pi w^2}\right)^2}\] qui permettent de retrouver la taille du waist et sa position en connaissant \(R\) et \(w\).