Étude de cas
Modes longitudinaux
Nous allons pour terminer déterminer les fréquences des modes longitudinaux de la cavité : le déphasage subi par l'onde sur un aller simple dans la cavité est égal à (voir cours): \[\Delta \phi = \phi (d) = \phi (0) = -k(D) + \zeta (d) - \zeta (0) = -q\pi\] avec \(k=2\pi \frac \nu c\), \(D\) le chemin optique parcouru \((D=L+nl)\), \(tan(\zeta(0))=0\), et \(tan(\zeta(d))=\frac d {Z_R} = \sqrt\frac d{R-d}\) .
Par conséquent : \[\nu _q = \frac c {2D} \left( q+\frac 1 \pi \left( arctan\left(\sqrt\frac d {R-d}\right)\right)\right)\] et pour les modes transverses : \[\nu _{mnq} = \frac c {2D} \left( q+\frac {m+n+1} \pi \left( arctan\left(\sqrt\frac d {R-d}\right)\right)\right)\]
On trouve en prenant \(L\) = 80 mm un écart entre deux modes longitudinaux de l'ordre de 1,5 GHz et un écart entre le mode fondamental et le premier mode transverse de 575 MHz (voir figure 7).
Remarque:
Pour que la longueur d'onde (1064 nm) corresponde à la fréquence relative à l'ordre \(q\), il faut que \(q\) vaille environ \(1,195.10^8\).
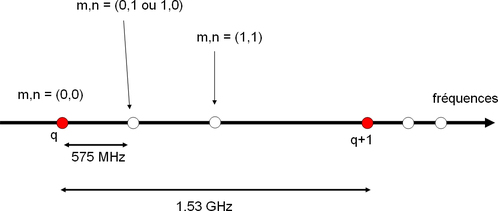
Figure 7 : Position des modes longitudinaux