Optique des LASER et faisceaux gaussiens
I. Les résonateurs ouverts
2. Intérêt et description des résonateurs ouverts
Introduction
Le rôle de la cavité laser est de permettre l'amplification répétée de l'onde optique grâce à un système réfléchissant (la plupart du temps des miroirs). C'est aussi la cavité qui permet, via ses pertes (un des miroirs utilisé n'est que partiellement réfléchissant), d'extraire le faisceau laser utile. Enfin la géométrie de la cavité détermine en grande partie les caractéristiques spatiales et spectrales du rayonnement laser émis.
Pourquoi un résonateur ouvert ?
Le résonateur le plus simple que l'on puisse imaginer est une boite parallélépipédique (fermée, donc) dont toutes les parois sont métallisées. Cette cavité possède un certain nombre de modes susceptibles d'osciller, et ces modes sont définis par les conditions aux limites sur les parois pour les vecteurs d'ondes (un mode est associé à un vecteur d'onde \(\vec k_{mnq}\) avec \(k_x = m \frac \pi a, k_y = n \frac \pi b, k_z = q \frac \pi d\) où \(a, b, d\) sont les dimensions du parallélépipède).
Si on insère un milieu amplificateur dans une telle cavité, les modes vont se mettre à osciller et on aura amplification. Cependant, pour que l'onde produite soit cohérente, il faut que le nombre de modes susceptibles d'osciller, c'est à dire compris dans la bande spectrale d'amplification du milieu amplificateur, soit faible.
Si on calcule le nombre de modes dans cette bande de fréquence \( \Delta \nu\), on trouve qu'il est proportionnel au volume de la cavité et inversement proportionnel à la longueur d'onde au carré. Numériquement, si la longueur d'onde vaut 10 cm (domaine des micro-ondes), alors une dizaine de modes sont susceptibles d'osciller dans une bande de 1 GHz et une cavité de dimensions raisonnables (10 cm de côté). Par contre, si la longueur d'onde appartient au domaine optique (par exemple 1 µm), alors on trouve pour cette cavité environ \(10^{11}\) modes dans la même bande spectrale.
C'est pour cela que de tels résonateurs sont très bien adaptés pour réaliser des MASERS (Microwave Amplification by Stimulated Emission of Radiation) mais ne sont pas utilisables avec de la lumière visible : un trop grand nombre de modes vont osciller simultanément, ou, en d'autres termes, la taille de la cavité nécessaire pour obtenir un fonctionnement quasi-monomode est micrométrique.
Remarque:
Avec la technologie actuelle, ce type de micro-cavité est réalisable – ce qui n'était pas le cas en 1960 – néanmoins, le milieu amplificateur est dans ce cas trop petit pour espérer réaliser des sources puissantes.
Il est donc nécessaire de modifier la géométrie du résonateur : l'idée proposée et développée, entre autre par Schallow et Townes dans les années 50, consiste à utiliser un résonateur quasi-linéaire où une seule direction d'oscillation est permise : c'est le résonateur ouvert, constitué dans sa forme la plus simple de deux miroirs face à face dans une configuration d'interféromètre de Fabry-Pérot.
En première approche, les modes d'un tel résonateurs sont similaires à ceux décrits pour la cavité fermée si on fait l'hypothèse que \(d\gg a, b\). Une telle structure réduit considérablement le nombre de modes susceptibles d'osciller, comme on s'en rend compte avec le Fabry-Pérot : tous les rayons qui présentent un angle trop important par rapport à l'axe de la cavité vont rapidement sortir de cette dernière. Dans le cas du Fabry-Pérot, néanmoins, le moindre défaut de parallélisme va faire sortir tout faisceau de la cavité après quelques aller-retours seulement. Pour qu'un laser fonctionne efficacement, et que la cavité joue son rôle de filtre spatial et spectral, il faut que certains rayons restent dans la cavité assez longtemps : on a besoin de cavités stables, nous y reviendrons.
Description des résonateurs
La cavité la plus simple pouvant être stable est la cavité linéaire constituée de deux miroirs face à face, de rayons de courbure \(R_1\) et \(R_2\), distants d'une distance \(L\), et de diamètres respectifs \(D_1\) et \(D_2\) (voir figure 1). Dans ce type de cavité, une onde stationnaire est formée. Elle peut également contenir divers éléments optiques (des lentilles, des éléments polarisants, des composants actifs...) : on appelle « cavité passive » la cavité sans son milieu amplificateur, par opposition à la cavité active où le milieu amplificateur est présent.
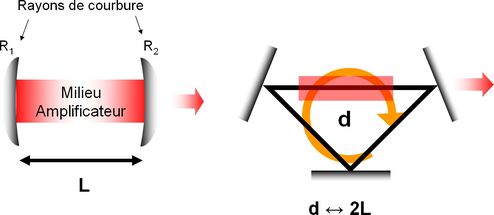
Figure 1 : Cavité linéaire et cavité en anneau
Remarque:
Ce qui nous intéressera par la suite est le chemin optique [d] parcouru par la lumière lors d'un aller-retour dans la cavité, Ce chemin optique est défini comme le produit de la distance parcourue par l'indice de réfraction rencontré par la lumière.
Remarque:
Un autre type de cavité répandu est la cavité en anneau (voir figure 1), où la lumière ne revient pas sur elle-même mais forme une onde progressive. Dans ce cours, on se limitera en général à la cavité linéaire, mais les raisonnements et les méthodes utilisés sont valables pour tout résonateur.