Optique des LASER et faisceaux gaussiens
II. Stabilité des cavités lasers
3. Matrices de transfert et loi ABCD
Introduction
Même s'il est possible d'obtenir un laser avec des cavités instables dans certains cas bien particuliers (voir plus loin), il est en général préférable d'avoir une cavité stable. L'étude théorique de la stabilité est indispensable pour dimensionner la cavité (choix des rayons de courbure, des distances) avant de commencer à la construire.
Les matrices de transfert
L'étude de la stabilité de la cavité sera faite en utilisant la notion de matrice de transfert (ou matrices ABCD).
Le principe de cette méthode est d'associer à chaque élément optique au sens large (simple propagation dans un milieu donné, lentille, miroir...) une matrice 2x2 spécifique. On pourra ainsi déterminer les caractéristiques liées à la propagation par simple multiplication des matrices élémentaires.
Considérons une propagation dans le plan \(yOz\), l'axe \(z\) étant celui de la cavité. Dans ce plan, un rayon donné est caractérisé par son ordonnée de départ \(h\) et par la pente \(\theta\) de la droite qui supporte le rayon paraxial (voir figure 5).
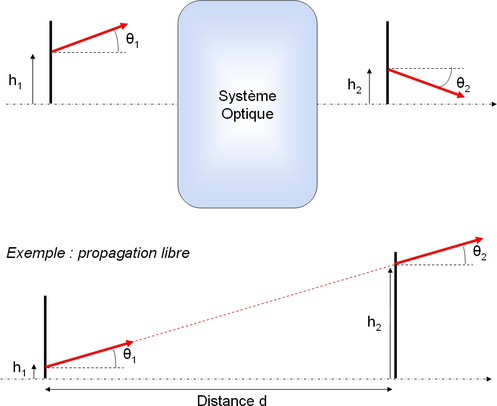
Figure 5 : Définition des paramètres
Dans les conditions de Gauss, les relations entre \( (h_1 , \theta_1)\) avant la traversée d'un système optique donné et \( (h_2 , \theta_2)\) après cette traversée sont linéaires et peuvent s'écrire sous forme matricielle : \[ \begin{pmatrix} h_2 \\ \theta_2 \\ \end{pmatrix} = \begin{pmatrix} A & B \\ C & D \\ \end{pmatrix} \begin{pmatrix} h_1 \\ \theta_1 \\ \end{pmatrix}\] où les termes diagonaux sont sans dimension, B et C ayant respectivement les dimensions d'une longueur et de l'inverse d'une longueur.
La matrice \( T = \begin{pmatrix} A & B \\ C & D \\ \end{pmatrix}\) caractérise complètement le système optique traversé.
Nous allons maintenant déterminer les matrices ABCD pour quelques composants essentiels d'une cavité, et montrer comment obtenir la matrice ABCD du système complet à partir de ces composants élémentaires.
- Propagation sur une distance \(d\) :
\( T = \begin{pmatrix} 1 & d \\ 0 & 1 \\ \end{pmatrix}\), la démonstration est évidente (voir figure 5) :
\(h_2=h_1 + d \theta_2\) et \(\theta_2 =\theta_1\)(les rayons étant paraxiaux, on assimile l'angle à sa tangente).
Or en développant l'expression matricielle ci-dessus: \( \begin{matrix} h_2=Ah_1+B\theta_1 \\ \theta_2 = Ch_1 +D\theta_1 \\ \end{matrix}\)
On en déduit par identification termes à termes : \(A =1, B=d, C=0, D=1\).
Nous ne démontrerons pas les autres relations (le raisonnement est exactement le même) : cela pourra être fait sous forme d'exercice.
Propagation sur une distance d dans un milieu d'indice \(n\):
\[ T = \begin{pmatrix} 1 & \frac d n \\ 0 & 1 \\ \end{pmatrix}\]
Dioptre plan entre deux milieux d'indices \(n_1\) et \(n_2\):
\[ T = \begin{pmatrix} 1 &0 \\ 0 & {\frac{n_1}{n_2}} \\ \end{pmatrix}\]
Lentille mince de distance focale \(f\):
\[ T = \begin{pmatrix} 1 & 0 \\ -\frac 1 f & 1 \\ \end{pmatrix}\]
Miroir concave ou convexe de courbure \(R\):
\[ T = \begin{pmatrix} 1 & 0 \\ {-\frac{2}{R}} & 1 \\ \end{pmatrix}\]
On retrouve bien sûr l'équivalence miroir-lentille avec \(R=2f\) (voir plus haut).
Attention:
De manière générale, pour \(N\) systèmes optiques successifs \(S_i (i=1,2,...,N)\) ayant chacun une matrice \(T_i\), la matrice de l'ensemble est le produit des matrices dans l'ordre inverse : \(T_{systeme}= T_N...T_i...T_3T_2T_1\)
Attention, en général les matrices ne commutent pas et l'ordre doit être strictement conservé.
La matrice \(T\) est unitaire (son déterminant vaut 1), sauf dans le cas (rare) où le milieu de départ et le milieu d'arrivé ont des indices différents.
On verra par la suite que cette méthode matricielle s'applique non seulement en optique géométrique mais également pour les faisceaux gaussiens
Remarque:
Il arrive souvent que des systèmes astigmates soient introduits dans les cavités lasers (miroirs sphériques hors d'axe, lames à incidence de Brewster, lentilles cylindriques, prismes...). Dans ce cas, il existe un comportement différent suivant les deux directions orthogonales. Il faut alors distinguer les matrices ABCD dans la direction \(x\) et celles dans la direction \(y\).
La loi ABCD
Elle permet de décrire la propagation d'une onde sphérique dans un système optique.
Considérons une onde sphérique issue d'un point \(O_1\), avec un rayon de courbure \(R_1\) à l'entrée d'un système optique donné et convergeant en un point \(O_2\) avec un rayon de courbure \(R_2\) à la sortie de ce système. On prendra comme convention : \(R>0\) lorsque l'onde diverge et R<0 lorsque l'onde converge.
On a dans ces conditions \(R_1 \approx \frac {h_1}{\theta_1}\) et \(R_2 \approx \frac {h_2}{\theta_2}\) (voir figure 6)
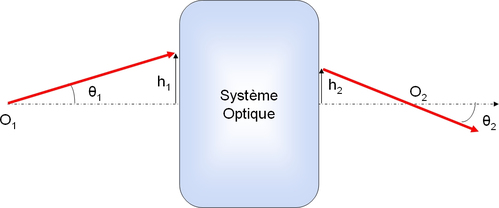
Figure 6 : Paramètres pour la démonstration de la loi ABCD
On peut donc déduire à partir de la définition de la matrice ABCD :\[R_2 = \frac{AR_1 + B}{CR_1 + D}\]
C'est la loi ABCD
Cette loi est très importante, notamment parce qu'on la généralisera au cas des rayons de courbure complexes (voir plus loin le chapitre sur les faisceaux gaussiens).